前言
边缘提取
RANSAC直线拟合算法
5. 提取与跟踪的结果

前言

我的目标是，在连续的两帧影像上，根据前一帧影像的已知直线，在下一张影像上找到对应的直线位置。

假设每一帧影像的标号为1,2,3,4,5…，直线L1在影像1上的位置是已知的，并且在影像2上存在一个缓冲区，影像2上的L1位于这个缓冲区内。

预测缓冲区的方法较为多样。如果已知物体的旋转角速度和运动速度，以及运动相机的运动状态，可以直接计算出目标在影像上的像素偏移量和旋转角度；也可以先对目标进行点匹配，筛选出正确率较高的匹配点，根据匹配点之间的偏移平均值、两个匹配点连成的直线的夹角、均匀分布的匹配点的中心，计算出每一条直线对应的缓冲区的仿射变换（旋转、平移、伸缩）参数，进而预测出缓冲区的位置；或者使用光流法（Optical Flow）进行跟踪和预测，目前正在研究中。

获取缓冲区后，首先对缓冲区进行边缘提取，接着在一系列的边缘点中，提取出目标直线。

在这篇文章中，我将介绍边缘提取方法和基于统计与误差思想的RANSAC直线提取方法。

边缘提取

边缘提取的方法包括：

使用一阶微分/二阶微分算子进行卷积运算提取，如：Sobel算子、Prewitt算子、Robert算子、Laplacian算子；
使用更加精细化的、可以提取到像素/子像素的方法，如：Canny方法。

考虑到像素/子像素级别的边缘提取方法会导致边缘强度信息丢失，难以进一步提取直线，因此我使用的是可以提取较粗边缘、保留较好强度信息的一阶微分卷积算法（Sobel算子）。

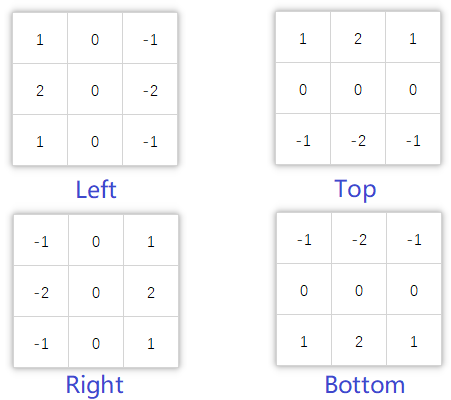
使用四个方向的Sobel算子分别对灰度图进行卷积运算，接着将卷积后的四幅影像取绝对值后相加取平均，得到具有一定宽度和亮度的边缘。

// 用sobel算子提取边缘（四个方向）
Mat sobelTop, sobelBottom, sobelLeft, sobelRight;
sobelLeft = (Mat_<float>(3, 3) <<
    1, 0, -1,
    2, 0, -2,
    1, 0, -1);
sobelRight = (Mat_<float>(3, 3) <<
    -1, 0, 1,
    -2, 0, 2,
    -1, 0, 1);
sobelTop = (Mat_<float>(3, 3) <<
    1, 2, 1,
    0, 0, 0,
    -1, -2, -1);
sobelBottom = (Mat_<float>(3, 3) <<
    -1, -2, -1,
    0, 0, 0,
    1, 2, 1);
Mat gt, gb, gl, gr;
filter2D(gray, gt, CV_32FC1, sobelTop);
filter2D(gray, gb, CV_32FC1, sobelBottom);
filter2D(gray, gl, CV_32FC1, sobelLeft);
filter2D(gray, gr, CV_32FC1, sobelRight);

Mat((abs(gt) + abs(gb) + abs(gl) + abs(gr)) / 4).convertTo(dst, CV_8UC1);

提取后的边缘如下图所示：

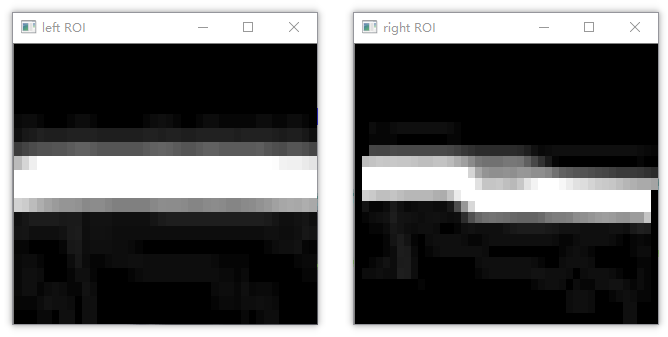
RANSAC直线拟合算法

提取具有强度信息的边缘后，需要通过这些边缘点拟合出一条直线，在这里我用到了RANSAC算法。

RANSAC为Random Sample Consensus（随机采样一致）的缩写，算法的思想是：根据一组包含异样数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据。它由Fischler和Bolles于1981年最先提出。

RANSAC基本思想描述如下：

考虑一个最小抽样集的势为n的模型（n为初始化模型参数所需要的最小样本数）和一个样本集P，集合P的样本数#(P)>n，从P中随机抽取包含n个样本的P的子集S初始化模型M；

余集SC=P\S中与模型M的误差小于某一设定阈值t的样本集以及S构成S*。S*认为是内点集，它们构成S的一致集(Consensus Set)；

若#(S*)≥N，认为得到正确的模型参数，并利用集S*(内点inliers)采用最小二乘等方法重新计算新的模型M*；重新随机抽取新的S，重复以上过程；

在完成一定的抽样次数后，若未找到一致集则算法失败，否则选取抽样后得到的最大一致集判断内外点，算法结束。

基于RANSAC的基本方法，我们可以进行一定的改进，借鉴统计与误差的思想，将其用于边缘图像的直线拟合。下面，将首先介绍该方法的总体流程，接着从种子点的选取、随机选取直线的数量、误差的计算方法三个方面详细论述。

1. 算法流程

对边缘图像进行归一化处理，使其亮度处在某一范围 $(a, b)$ 内；
在边缘图像中选取一系列种子点 $p_i,0 \leq i \lt N$ ，这些种子点与目标直线有着相似的分布，具有一定亮度信息；
从所有的种子点中随机选取两点（ $pt_1, pt_2$ ）拟合直线 $L$ ，获得直线参数 $a,b,c$ ；
分别计算每个种子点与直线 $L$ 的距离 $d_i$

$d_i=\frac{|ax_i+by_i+c|}{\sqrt{a^2+b^2}}$

考虑亮度 $I_i$ 与距离 $d_i$ ，计算直线 $L$ 与所有种子点之间的标准差 $\sigma$ ，其中，距离与误差成正比，亮度与误差成反比

$\sigma=\sqrt{\frac{\sum{\frac{d_i}{I_i}}}{N}}$

重复 $K$ 次3-5步的运算，找到所拟合出的直线 $L$ 具有最小标准差 $\sigma_\min$ 的两个点，这两个点所连接的直线即为目标直线。

2. 种子点的选取

在对直线的大致位置进行预测后，得到一个缓冲区，缓冲区的中心线与目标直线具有相似的分布。

选取种子点可以在缓冲区的中心线附近沿着直线方向进行查找。

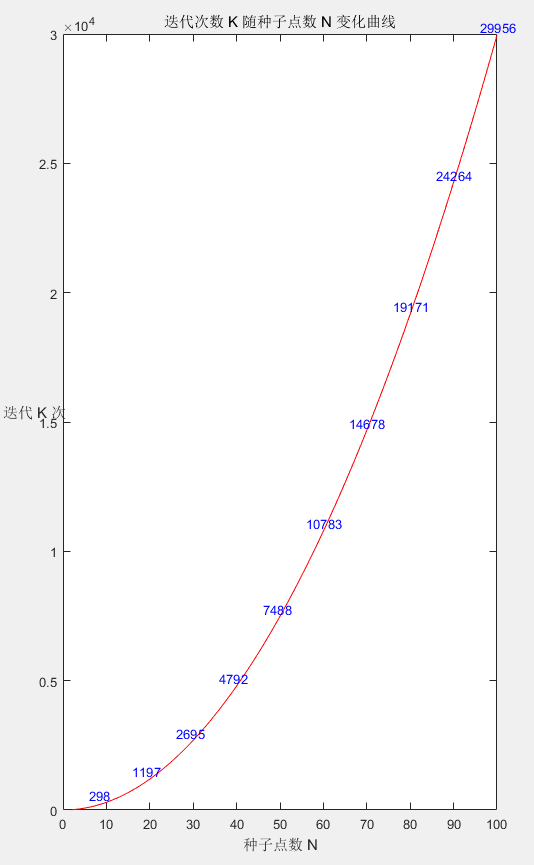
3. 随机选取直线的数量

假设有 $N$ 个种子点（ $N≥2$ ），其中包含两个最优的种子点，在所有点中随机选取，选中两个最优种子点的概率为 $q$

$q = (\frac{1}{N})^2$

在 $K$ 次迭代中，每次迭代随机选取两个点进行拟合，要求拟合的所有直线中，包含最优直线的概率为 $P$ ，则

$P = 1-(1-q)^K = 1-(1-(\frac{1}{N})^2)^K$ $K = \frac{log(1-P)}{log(1-q)} = \frac{log(1-P)}{log(1-(\frac{1}{N})^2)}$

迭代次数K随种子点数N变化的曲线图如下所示（所有拟合直线中包含最优直线的概率 $P=0.95$ ）：

4. 误差的计算方法

在所有参与直线拟合的种子点中，与直线的距离越远，说明该点是内点的可能性越小，误差越大；同时，种子点的亮度越低，说明该点是边缘点的可能性越小，误差越大。因此可以得到单个种子点 $i$ 的误差计算公式：

$e_i=\frac{d_i}{I_i}$

其中， $d_i$ 是种子点 $i$ 到直线的距离， $I_i$ 是种子点的亮度值。直线整体误差的标准差 $\sigma$ 的计算公式为：

$\sigma=\sqrt{\frac{\sum^N_{i=1}{\frac{d_i}{I_i}}}{N}}$

03的开发日志

RANSAC算法在拟合边缘直线中的应用

前言